Numbers and simple algebraic equations for statistics

Numbers

The idea of a number is very interesting.  In the above image we see the integers 1, 2, and 3 being used to count.

Note. When we say “integer” we mean numbers like $0, 1, 2, 3, 4, \ldots$ and $-1, -2, -3, -4, \ldots$. The numbers $\frac{1}{3}, 150.5, \sqrt{2}, \pi$  aren’t integers.

Some things are very easy to count. Like how many marbles are in a bag, how many apples are in box, and so on.

Other things aren’t so easy to count or measure.

Example: Sometimes we’re asked to fill out a form, where we are asked to rate a movie or a product or even a math professor! Something like this:

Professor McCarthy 🙂

or this:

Professor McCarthy    🙁

But, what does each star represent? Is a four star rating twice as good as a two star rating? Also, some people are very critical, so they will never give a good rating. Other people are way too nice, and always give a good rating.

So, just because we can assign numbers (like a number of stars) to try to measure or rate some property, doesn’t mean that doing so makes complete sense.

On the other hand, it is very useful to be able to numerically rate products (or math professors). So, we assign ratings using numbers (or stars) and hope for the best.

Fractions

Fractions are very interesting numbers and super important in probability and statistics.

Example. Consider the fraction $\frac{3}{4}$.   What does $\frac{3}{4}$ mean? One way of thinking about $\frac{3}{4}$ is that it represents the following situation:

• • •   •

We have 4 marbles and 3 of them are green. So, we can write $\frac{3}{4}$ of the marbles are green. Now, let’s double the marbles:

• • •   •
• • •   •

Now we have $2 \times 4 = 8$ marbles, of which,  $2 \times 3 = 6$ are green. So, we can write $\frac{6}{8}$ of the marbles are green.

In both situations the “proportion” or “fraction” of marbles are the same. In other words we should have, as numbers,  $\frac{3}{4} = \frac{6}{8}$.

Mathematically, we define $\frac{a}{b} = \frac{c}{d}$ if and only if $ad = bc$.

In our example, we can see that $\frac{3}{4} = \frac{6}{8}$ because $(3)(8) = (4)(6) = 24$.

We can also check to see if two fractions are equal by turning the fractions into their decimal representative:

$\frac{3}{4} = \frac{6}{8} = 0.75.$

You can easily do that on a calculator by entering

and

and seeing that you get 0.75 both times.

You can do the same calculation using the (free) statistics software R as follows:

The important thing about fractions, for our class, is that a fraction between 0 and 1 is used to tell us what part of a whole has some property.

In the above example  $\frac{3}{4}$ of the marbles have the property of being green.

If we have 100 marbles and $\frac{3}{4}$ are green, we can find how many of the 100 marbles are green:

$\frac{3}{4} \times \text{(the 100 marbles)}  = 75$ green marbles.

It is easy to do this calculation by hand, but I like to use a calculator or computer.

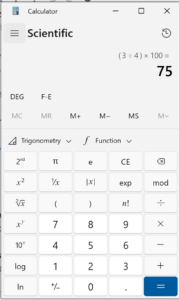
In a calculator you put and the output should be 75.

Remember, when entering complex expressions into a calculator, it is a good idea to put parenthesis to make sure the calculator does the calculation the way you want.

Algebra

For statistics it helps to know a little algebra.

The algebra we need is covered very nicely by BMCC’s (CUNY) Elementary Algebra website which is free for anyone to access online.  Here are the links to the sections of their Elementary Algebra website that are most relevant to Mat 150.5:

Please watch the videos (most of them are short) on the following pages.

Most importantly:
Chapter 1 — Foundations
Chapter 2 — Solving Linear Equations and Inequalities
Chapter 3 — Slope, Graph of a Line, and Finding the Equation of a Line

Example 1.  Suppose the area of rectangle is $18 \ \text{cm}^2$ and its base is $6 \ \text{cm}$. Find the height of that rectangle.

Answer.  The formula for the area $A$ of a rectangle is $$A = bh$$ where $b$ is the the length of its base and $h$ equals its height. We have to solve $A = bh$ for $h$. Here’s the math:

$\begin{align}
A &= bh  \quad \text{Now, divide both sides by b, get:}\\
\frac{A}{b} &= \frac{bh}{b} \quad \text{Now, cancel the b’s on the right side of the equation, get: }  \\
\frac{A}{b} &= h \\
\end{align}
$

So, for our rectangle we have $$h = \frac{A}{b} = \frac{18 \ \text{cm}^2}{6 \ \text{cm}} = \frac{18}{6}  \cdot \frac{ \text{cm}^2}{\text{cm}} = 3 \ \text{cm} = \text{answer}$$

Notice that  $$ \frac{ \text{cm}^2}{\text{cm}} =  \text{cm}$$.

Note. We can cancel the $b$’s in $\frac{bh}{b}$ because
$$\frac{bh}{b} = \frac{b}{b} \cdot \frac{h}{1} =  1 \cdot \frac{h}{1} = h$$

Example 2.  Consider the blue and yellow rectangle shown below. Suppose the area of the blue and yellow rectangle is $18 \ \text{cm}^2$ and that the area of the blue part of the rectangle $6 \ \text{cm}^2$.  Find the area of the yellow part of the rectangle.

Answer.  Let $A = $ the area of the blue and yellow rectangle. Let $B$ = area of the blue part of the rectangle. Let $Y$ = area of the yellow part of the rectangle. A formula for the area of the blue and yellow rectangle is $$A = B + Y$$

We have to solve for $Y$.  Here’s the math:

$\begin{align}
A &= B + Y  \quad \text{Now, subtract B from both sides, get:}\\
A – B &= B + Y – B \quad \text{Now, cancel the B’s on the right side of the equation, get: }  \\
A – B &= Y  \\
\end{align}
$

So, for our yellow rectangle we have $$Y = A – B =  18 \ \text{cm}^2 \ –  \  6 \ \text{cm}^2 = 12 \ \text{cm}^2 = \text{answer}$$

Note. We can cancel the $B$’s in $$B \ + \ Y \ – \ B$$ because
$$B \ – \  B \ =  \ 0$$

 

---