1. Set Theory

A set is just a collection of objects. The objects in the set are called members or elements.

It is common to denote the names of sets by a capital letter, like:

\displaystyle \ A, B, C, \ldots

We use curly brackets to denote a set. For example, the set A  consisting of the three elements a, b, c, could be written as:

\displaystyle \ A = \{a,b,c\}

To indicate that a, b and c are elements of the set A we can write:

\displaystyle \ a \in A, \ \ b \in A, \ \text{ and } \ c \in A

or more concisely, we can write:

\displaystyle \ a,b,c \in A

The symbol  \displaystyle \ \in   means “is an element of” or “in”. Note \displaystyle \ \in is the Greek letter epsilon.

The symbol \notin means “not an element of” or “not in”.

Example.  If A = {1, 2, 3}, then 4 \notin A .

The order in which we list the members of a set doesn’t matter, furthermore, if we list a member of a set more than once, it doesn’t mean that we have duplicates of that member. For example:

{a, b, c},    {c, b, a},    {a, a, b, c}

all mean the same thing: the set which consists of the three elements a, b, c.

Unions and Intersections

A \cup B = A \text{ union } B
A \cap B = A \text{ intersection } B

The above Figure shows an example of a union and an intersection

The Empty Set

The empty set is denoted:

\emptyset

The empty set is the set with no elements in it, so:

\emptyset = \{ \ \}

Subsets

The symbol:

\subset

means “subset of” or “contained in”.

A \subset B means every element of A is an element of B.

The above Figure shows an example of
A \subset S

Notes.

  1. By convention, the empty set is considered a subset of every set.
  2. If A is any set, then A \subset A is true.

Set minus

A \setminus B =   A minus B = all the elements of A that are not in B.

The symbol \setminus is called “set minus”.

We will also use the minus sign from arithmetic - to mean set minus. So, A - B means the same thing as A \setminus B .

Example.  If  A =  {a, b, c, d} and B = {c, d, e} then

A \setminus B = \{a, b\}

or, equivalently

A - B = \{a, b\}

 

Complements

If

A \subset S

then the complement of A (relative to S) is S minus A.  Complements are extremely important.  The complement of A is written as:

A^c = S \setminus A = S - A

Example.  If S = {a, b, c, d} and A = {a, b, c} then the complement of A relative to S is {d}.

Often we’ll just say “the complement” when it is clear from context what the complement is relative to.

Disjoint sets

Two sets are called disjoint if their intersection is empty.

The Size of a Set and Finite vs Infinite

The integers are the whole numbers: 0, 1, -1, 2, -2, 3, -3, . . .

The size of a set is how many elements are in that set.

Finite vs infinite: A set is called finite if its size is a non negative integer, like 0, 1, 2, . . .   A set is called infinite if its size isn’t finite.

The symbol for infinity  is \infty

The size of a set A is typically denoted |A|.

The size of a finite set is how many elements are in that set.

Example.  If A = {a, b, c} then the size of A is three because there are three elements in A. We would write:

|A| = 3

Example. The size of the empty set is zero.

Examples of infinite sets. The following sets are all infinite.

  • The set of integers:     0, 1, -1, 2, -2, 3, -3,  . . .
  • The set of positive integers:    1, 2, 3,  . . .
  • The set of positive even integers:   2, 4, 6, 8, 10, . . .
  • The real numbers (the number line is a “picture” of the real numbers; the real numbers include all the integers, all the fractions, all the decimal numbers).
  • [0, 1] = the numbers between 0 and 1 (including 0 and 1).  This is an infinite set because there is an infinite amount of numbers between 0 and 1.  For example, the set 1/2,  1/3,  1/4, 1/5, . . . and the set 0.1, 0.12, 0.123, . . . are both infinite sets of numbers and both are contained in [0, 1].
  • (0, 1) = the numbers strictly between 0 and 1. The set (0, 1) doesn’t include 0 and 1. The set (0, 1) is infinite for same reason that [0, 1] is infinite.

 

The Counting Theorem

Counting Theorem.  If A and B are finite sets then

|A \cup B| = |A| + |B| - |A \cap B|

Proof. If we count the elements in A and the elements in B we will have counted
the elements in

A \cap B

twice, so we need to remove (subtract) one copy of A \cap B.

Hence, the Counting Theorem is proven.

Example:  If A = {a, b, c } and B = {b, c, d }, then

|A \cup B| = |\{a,b,c,d \}| = 4

which agrees with the Counting Theorem since:

|A \cup B| = |A| + |B| - |A \cap B| = 3 + 3 - 2 = 4

because:

|A \cap B| = |\{b,c \}| = 2

 

Corollary to the Counting Theorem.  If A and B are finite disjoint sets then

|A \cup B| = |A| + |B|.

Proof.  If A and B are disjoint, then A \cap B is the empty set. The size of the empty set is 0. So, the Counting Theorem becomes:

|A \cup B| = |A| + |B| - |A \cap B| = |A| + |B| - 0 = |A| + |B|

Hence, the Corollary to the Counting Theorem is proven.

Example.

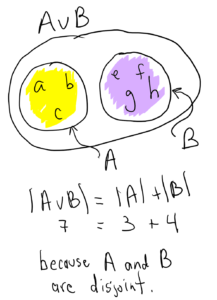
Example. If A = {a, b, c} and B = {d, e, f, g} then

|A \cup B| = |A| + |B| = 3 + 4 = 7

because A and B are disjoint (they don’t overlap, their intersection is empty).

 

Functions

We say f is function from the set A to the set B if f associates each element of A with one element of B. The set A is called the domain of f and the set B is called the range of f. We often write f : A \rightarrow B , which we read as “f maps A to B”, and which means f is a function with domain A and range B. We write f(a) = b if b is the element of B that f associates with a.

We often use the letters f, g , x, X, y, Y, to denote functions.

Examples of functions.

  • A = B = the real numbers and define f by the formula  f(x) = 2x + 3. In this example f is the name of the function and x is the name of the variable. To know what number in the range is associated with a number x in the domain, we just substitute x into the formula. For example, f(10) = 2(10) + 3 = 23. So, f associates the number 23 (which is in the range of f) with the number 10 (which is in the domain of f). Usually we just say “f of 10 is 23”.
  • A = the real numbers. B = the non negative real numbers, and define f by the formula f(x) = x^2 .  In this example f is the name of the function and x is the name of the variable.
  • A = {a, b, c} and B = { 1, 2, 3, 4}. Define f as follows.
    f(a) = 1
    f(b) = 2
    f(c) = 2
  • A = {a, b, c} and B = { 1, 2, 3, 4}. The following would NOT be a function because f(a) equals two different values.
    f(a) = 1
    f(a) = 2  (we can’t have f(a) equaling two different values if f is a function)
    f(b) = 3
    f(c) = 4
  • S = {HH, HT, TH, TT}.   Define X to be the function that counts H’s. So,
    X(HH) = 2
    X(HT) = X(TH) = 1
    X(TT) = 0
    In the above example we only gave the domain of the function X, which is S.  We didn’t say what the range is. Technically, we should say what the range is, but often we don’t. The reason is that for many calculations, you don’t need to know precisely what the range is.

For more information on functions see the Wikipedia entry for functions:
https://en.wikipedia.org/wiki/Function_(mathematics)

Inverse and Preimage of a Function

If f:A \rightarrow B and b \in B , the preimage or inverse of b (with respect to f) is:

f^{-1}(b) = \{ a \in A \mid f(a) = b \}

which is the mathematical notation for saying “the set of all a \in A such that f(a) = b .  The vertical line means “such that”.

Example. If f(x) = x^2 then f^{-1}(25) = \{ -5, 5 \} because f(-5) = (-5)^2 = 25 and f(5) = 5^2 = 25 .

Example. Suppose S = {HH, HT, TH, TT} and X is the function on S which counts H’s. Then

X^{-1}(0) = \{TT \}
X^{-1}(1) = \{HT, TH \}
X^{-1}(2) = \{HH \}

Notation. Sometimes, especially in statistics, instead of using the inverse-style notation f^{-1}(b)   we use the notation f = b to indicate the preimage of b with respect to f.

Example. Suppose f(x) = x^2 .  If we write f = 25, we mean the set f^{-1}(25) = \{ -5, 5 \} .