The following video (12 minutes with 8 questions solved) will help you with your Blackboard homework on this unit.

Counting Principles

Note. Some of the mathematics might not display properly on your cell phone. If this is the case, try viewing in landscape mode, or better yet, on a regular computer screen.

Multiplication Principle

Question 1. Suppose we have 3 pants:

Pants = {Red, White,  Blue}

and 2 shirts:

Shirts = {Green, Yellow}

How many different (pants, shirts) combinations can we make?

Answer to Question 1.  3 x 2 = 6 combinations.  There are 3 choices for pants and 2 choices for shirts so there are 3 x 2 = 6 different (pants, shirts) combinations.

We can easily write down all 6 combinations by creating a 3 x 2 table. See Figure below.

Figure for Question 2. We can think of multiplication as telling us how many cells are in a table.

Set Multiplication
(Product of sets)

We can also think of Question 1 in terms of  set multiplication:

Pants $\times$ Shirts
= {R, W,  B} $\times$ {G, Y}
= { RG, RY, WY, WY, BG, BY }
So, we see that

|Pants $\times$ Shirts|
= |Pants| $\times$ |Shirts|
= $3 \times 2
= 6$

Question 2.  Suppose we have 3 different pants, 2 different shirts, 4 different hats. How many different (pants, shirt, hat) combinations can we make.

Answer to Question 2.  There are 3 x 2 x 4 = 24 different (pants, shirt, hat) combinations.

Permutations

A permutation of an ordered set or list is a rearrangement or a reordering of that set.

Example:  One permutation of:

1, 2, 3

is

3, 1, 2

another is

1, 3, 2

 

nPr Formula

The nPr formula tells us how many ways we can chose a subset of size r from a set of size n, if the order that we choose the r elements matters.

$$nPr =   \underbrace{n(n-1)(n-2)\cdots(n-r+1)}_{r \ terms} $$

The P in nPr stands for “permute” or “permutation”.

See Question 3 for an explanatory example.

Question 3. We have 4 letters:  {A, B, C, D}.  How many ways can we choose 2 of them if the order matters? Note. Since order matters, AB and BA are considered different.

Answer to 3. There are 4 choices for the first letter. After you chose the first letter, there are 3 remaining letters to choose from. So, there are 4 x 3 = 12 ways.  See Figure below. We can also use the nPr formula:

$$4P2 =   \underbrace{(4)(3)}_{2 \ terms} = 12 $$

Figure for Question 3

Question 4. Suppose there are 30 students in a class. The professor has a ticket for a baseball game, a football game, and basketball game. The professor will randomly select three students who will each get one of the tickets. How many possible outcomes are there?

Answer to Question 4. There are 30P3 = (30)(29)(28) = 24,360 possible outcomes.

n! (n factorial)

nPn is how many ways n objects can be permuted.

nPn is so important that it has its own symbol, which is “!”, in other words, nPn = n!

The ! is the factorial symbol. So, n! is “n factorial”.

$$n! =   \underbrace{n(n-1)(n-2)\cdots(3)(2)(1)}_{n \ terms} $$

Note, it is convenient to define:

0! = 1

so:

0! = 1
1! = 1
2! = 2 x 1 = 2
3! = 3 x 2 x 1 = 6
4! = 4 x 3 x 2 x 1 = 24
5! = 5 x 4 x 3 x 2 x 1 = 120
etc.

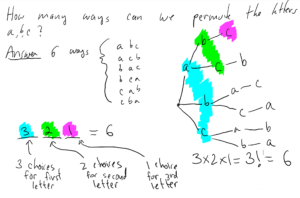
Question 5. How many different ways can we permute (rearrange) the letters a,b,c?

Answer to Question 5. There are 3 different letters so there are  $3! = (3)(2)(1) = 6$ permutations.  See Figure below.

Question 6. How many different ways can the numbers 1, 2, 3, 4, 5 be permuted?

Answer to Question 6.  We can permute them 5! = (5)(4)(3)(2)(1) = 120 different ways.

nCr

The C in nCr stands for “choose”. We pronounce nCr as “n choose r” or as simply, ” n c r”.

nCr = how many subsets of size r are contained in set of size n

or, equivalently

nCr = how many ways we can choose r objects from n objects if the order we choose doesn’t matter

The formula for nCr is given by:

$$ nCr =  \dfrac{n(n-1)(n-2)\cdots(3)(2)(1)}{r(r-1)(r-2)\cdots(3)(2)(1)} $$

The above formula for nCr is equivalent to:

$$ nCr =  \dfrac{nPr}{r!}  $$

and to

$$ nCr =  \dfrac{n!}{r! (n-r)!}  $$

Often, instead of using the letter r mathematicians will use the letter k and so instead of saying “n choose r” they will say “n choose k”. It means the same thing and has the same formula.

Notation. Sometimes mathematicians will write

$$\binom{n}{r} \text{ or }  \binom{n}{k} $$

instead of nCr or “n choose k”.

Note that numerically:

$$nC0 = nCn = 1$$

More generally, we have the:

Important nCr identity

$$\,_{n}C_{r} = \,_{n}C_{n-r} $$

The above identity easily follows from the complement principle. The following Figure indicates why the above identity is true for the case of 5C3 = 5C2.

In the above Figure, the choice of {A,C, D} (from 5C3) corresponds to the choice of {B, E} from 5C2.

Example.  Calculate 6C4

Answer. We can calculate 6C4 directly:

$$ 6C4 =  \dfrac{(6)(5)(4)(3)}{(4)(3)(2)(1)} = 15 $$

or we can use the identity 6C4 = 6C2 and then calculate 6C2 (which is easier to calculate than 6C4.

$$ 6C2 =  \dfrac{(6)(5)}{(2)(1)} = 15 $$

Derivation of nCr formula

We derive the nCr formula by writing the nPr formula in terms of the nCr formula. Here are some more details. Recall that:

nPr = how many ways we can choose r objects from n objects if the order we choose matters

r! = how many ways we order (or permute) r objects.

If we wanted to list all the nPr ways we can choose r objects from n objects if order matters, we could do it like this.  First we list all the subsets of size r that are in the set of size n. There are nCr such subsets.  Then, for each of those subsets of size r  we list all the possible permutations: there are r! such permutations.  So, there are nCr subsets or size r and each of these can be ordered (permuted) r! different ways. So, using the multiplication principle we have:

$$ nPr = nCr \times r!$$

which implies

$$nCr = \dfrac{nPr}{r!}$$

nCr Questions and Calculations

Question. How many ways can we choose 2 letters from A, B, C, D if order matters and if order doesn’t matter?

Answer.
If order matters there are 4P2 = (4)(3) = 12 ways.
If order doesn’t matter there are

$$ 4C2 = \dfrac{4P2}{2!} = \dfrac{(4)(3)}{(2)(1)} = 6  \ \text{ways}$$

Question. How many subsets of size 3 are in the set {A, B, C, D}?

Answer. The size of the set is n = 4 and the size of the subset is r = 3. There are nCr subsets of size r in a set of size n. So, the answer is:

$$ 4C3 = \dfrac{4P3}{3!} = \dfrac{(4)(3)(2)}{(3)(2)(1)} = 4 \ \text{subsets of size 3}$$

Question. Calculate 8C3.

Answer.

$$ 8C3 = \dfrac{8P3}{3!} = \dfrac{(8)(7)(6)}{(3)(2)(1)} = 56 \ \text{subsets of size 3}$$

Notice that in the numerator and in the denominator of

$$ 8C3 = \dfrac{(8)(7)(6)}{(3)(2)(1)}$$

there are 3 terms.

The numerator always starts at n (in the above Question n = 8) and goes down r  times (in the above Question r = 3) and goes down r = 3 times.  nCr is always like that. nCr always has r terms in the numerator and r terms in the denominator. (Unless r = 0, in which case, we just memorize that nC0 = 1).

Question. Suppose we sample 6 times with replacement from a bag with blue and white marbles in it.  How many ways can we get 4 blue marbles in our sample of size 6.
(What we mean is exactly 4 blue marbles.)

Answer.

$$ 6C4 = \dfrac{6P4}{4!} = \dfrac{(6)(5)(4)(3)}{(4)(3)(2)(1)} = 15 $$

Notice that in the numerator and in the denominator of

$$ 6C4 = \dfrac{(6)(5)(4)(3)}{(4)(3)(2)(1)}$$

there are 4 terms.

Important note about calculating nCr

An easy way to calculate nCr is to use your scientific calculator’s nCr function (button).

Unfortunately, each scientific calculator has its own unique way of accessing nCr.   You need to look in your calculator’s user manual (which you can usually find online) for instructions.

To calculate nCr in R we use the “choose” function. So, in R,

nCr = choose(n,r)

Question. Calculate 5C3 using R.

Answer.

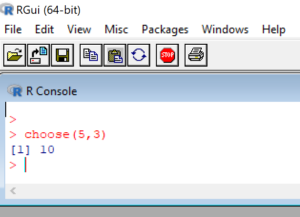
In R enter:

choose(5,3)

R will output the answer

10

So, 5C3 = 10.

We could easily calculate 5C3 directly:

$$ 5C3 = \dfrac{(5)(4)(3)}{(3)(2)(1)} = 10$$

Or, use the identiy, 5C3 = 5C2 and then

$$ 5C2 = \dfrac{(5)(4)}{(2)(1)} = 10$$