The following 5 videos (run times are from about 1 to 5 minutes each) will help you with your Blackboard homework on this unit.
Please scroll down past these homework videos for in depth explanation of these topics and the Standard Normal Distribution.
The Standard Normal Distribution
The traditional way of finding normal distribution probabilities uses the standard normal distribution look-up table instead of R.
The standard normal distribution, which is always referred to by the letter $z$, is the normal distribution with $\mu = 0$ and $\sigma = 1$. In other words:
$z \sim N(0, 1)$
Here is a picture of the standard normal distribution‘s PDF with the region under the PDF shaded a yellowish tan color:
 The “standard normal distribution” (also known as the z-distribution )
The “standard normal distribution” (also known as the z-distribution )
The z look-up table gives you the cumulative areas $A(z)$. Cumulative area means all the area under the PDF from $-\infty$ to $z$.
The z look up table consists of two pages. The first page is for negative z scores, the second page is for positive z scores.
Use the controls at the bottom of the embedded z-distribution look-up table
to navigate between its
first and second page.
Download link is under the embedded z-table.
It is easiest to understand how to use the z-table by watching the following videos:
Question 2. Using the z-table, find $P(z < 1.23)$.
Answer to Question 2. See video:
Note. In the above video we used page 2 of the z-table.
Question 3. Find the probability that $z < -0.54$.
Answer to Question 3. Using the z-table (page 1) we get:
$P(z < -0.54) = A(-0.54) = 0.2946$.
See Figures below.
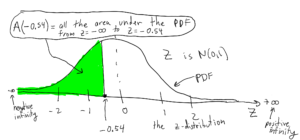
Using the z-distribution look-up table of cumulative areas we get:

Using R to find A(z) instead of the z-table
The R command:
pnorm(z)
returns A(z) from the z-table.
The following R script calculates A(-0.54) from the previous question.
# Find A(z) using R (instead of z table) z = -0.54; pnorm(z); # End of Script
R returns:
0.2945985
which, when rounded to 4 significant digits is 0.2946, same as the answer we got using the z-table.
Notes about $A(z)$
$A(z) = $ the cumulative area under the PDF of the standard normal distribution. We start accumulating area at the left end of the number line. We denote the left end of the number line as “negative infinity” which we write as $-\infty$. So, $A(-\infty) = 0$, because no area has accumulated yet. $A(\infty) = 1$ because the total area under any PDF is always 1. Finally, $A(0) = \frac{1}{2} = 0.5$ because when $z$ reaches 0, we are in the middle of the PDF for the z-distribution.
Finding areas (probabilities) for the z-distribution
$\mathbf{P(a < z < b)}$
The z-table gives us cumulative areas. So, to find a probability of the form $P(a < z < b)$ we need to subtract off the left tail, which is $A(a)$, from $A(b)$:
$P(a < z < b) = A(b) – A(a)$
Question 4. $z$ is $N(0,1)$. Find $P( -1.75 < z < 1.25 )$. Draw $z$ and shade the region corresponding to $P( -1.75 < z < 1.25 )$.
Answer to Question 4.
The following 6 minute long video shows how to do Question 4.

The above Figure, drawn by hand, shows the standard normal distribution $z$ and the region corresponding to $P( -1.75 < z < 1.25 )$.
Calculation:
$P(-1.75 < z < 1.25)$
$= A(1.25) – A(-1.75)$
$ = .8944 – .0401$
$ = .8543$

The Figure above, drawn by R, shows the standard normal distribution $z$ and the region corresponding to $P( -1.75 < z < 1.25 )$.
Here is how to find $A(1.25)$ and $A(-1.75)$ using the z-table.
The value for $A(1.25)$ is where the row for $z = 1.2$ and the column for $.05$ intersect.

The value for $A(-1.75)$ is where the row for $z = -1.7$ and the column for $.05$ intersect.

We can also solve this problem using the following R script. If we use R we don’t have to look up the values for $A(z)$ in the z-table:
# P(a < z < b) a = -1.75; b = 1.25; #-------------- pnorm(b); #A(b) from z table pnorm(a); #A(a) from z table pnorm(b)- pnorm(a); # End of script
The above R script outputs the cumulative areas $A(1.25)$ and $A(-1.75)$ (from the z-table) and then subtracts them to give us the numerical solution to Question 4.

Note. The cumulative areas $A(z)$ in the z-table are rounded to 4 decimal places, whereas R gives the cumulative areas to about 8 decimal places.
End of Answer to Question 4.
Question 5. $z$ is $N(0,1)$. Find $P( 0.75 < z < 1.25 )$. Draw $z$ and shade the region corresponding to $P( 0.75 < z < 1.25 )$.
Answer to Question 5.

Question 6. $z$ is $N(0,1)$. Find $P( -2.12 < z < -0.34 )$. Draw $z$ and shade the region corresponding to $P( -2.12 < z < -0.34)$.
Answer to Question 6.

Question 7. $z$ is $N(0,1)$. Find $P( -2.00 < z < 2.00 )$. Draw $z$ and shade the region corresponding to $P( -2.00 < z < 2.00)$.
Answer to Question 7.

Note about Question 7. $P( -2.00 < z < 2.00) = 95.44\% = $ the probability that z is within 2 standard deviations of the mean.
Question 8. $z$ is $N(0,1)$. Find $P( 0.00 < z < 1.00 )$. Draw $z$ and shade the region corresponding to $P( 0.00 < z < 1.00)$.
Answer to Question 8.

Finding areas (probabilities) for the z-distribution
$\mathbf{P(a < z)}$
The z-table gives us cumulative areas under the PDF. The total cumulative area is 1. So:
$P(a < z) = 1 – A(a)$
Note. $P(a < z) = P(z > a)$ because $a < z$ and $z > a$ mean exactly the same thing. I is very common to write $P(z > a)$ rather than $P(a < z)$
Question 9. $z$ is $N(0,1)$. Find $P( -1.43 < z )$. Draw $z$ and shade the region corresponding to $P( -1.43 < z)$.
Answer to Question 9.

Question 10. $z$ is $N(0,1)$. Find $P( z > 2.00 )$. Draw $z$ and shade the region corresponding to $P(z > 2.00)$.
Answer to Question 10.

Question 11. $z$ is $N(0,1)$. Find $P(z > 0)$. Draw $z$ and shade the region corresponding to $P(z > 0)$.
Answer to Question 11.

Question 12. $z$ is $N(0,1)$. Find $P( z > 1.52)$. Draw $z$ and shade the region corresponding to $P(z > 1.52)$.
Answer to Question 12.

Finding areas (probabilities) for the z-distribution
$\mathbf{P(z < b)}$
The z-table gives us cumulative areas under the PDF. So:
$P(z < b) = A(b)$
Question 13. $z$ is $N(0,1)$. Find $P( z < 1.64)$. Draw $z$ and shade the region corresponding to $P( z < 1.64)$.
Answer to Question 13.

Question 14. $z$ is $N(0,1)$. Find $P( z < 0)$. Draw $z$ and shade the region corresponding to $P( z < 0)$.
Answer to Question 14.

Question 15. $z$ is $N(0,1)$. Find $P( z < -2)$. Draw $z$ and shade the region corresponding to $P( z < -2)$.
Answer to Question 15.

The z-score and z-transformation theorem
Suppose $x$ is $N(\mu_x, \sigma_x)$ we define the z-transformation of $x$ as
$$z(x) = \dfrac{x – \mu_x}{\sigma_x}$$
The z-transformation theorem (proof below) says that $z(x)$ is $N(0,1)$ and
$$P(a < x < b) = P(z(a) < z < z(b))$$
In other words, we can find $P(a < x < b)$ using the z-table if we transform $a$ into $z(a)$ and $b$ into $z(b)$.
$z(a)$ and $z(b)$ are called z-scores.
The z-score $z(x)$ tells you how many standard deviations $x$ is from $\mu_x$.
Examples.
If $x \sim N(20, 4)$ then $z(24) = 1.00$ because $24$ is one standard deviation above the mean.
If $x \sim N(30, 5)$ then $z(25) = -1.00$ because $25$ is one standard deviation below the mean.
It sounds complicated, but it is actually easy. See Question 16 below.
z-scores and relative size
The z-score
$$z(x) = \dfrac{x – \mu_x}{\sigma_x}$$
gives us a uniform way to measure how big or small something is within its category. For example. A human who weighs 300 pounds would be considered big; an elephant that weighs 300 pounds would be considered small.
Example. Who’s relatively taller? A giraffe that is 5.5 meters (18 feet) tall or a man who is 2.0 meters (6 feet 7 inches) tall?
Giraffe heights are (approximately) normally distributed with a mean of $\mu = 5$ meters and a standard deviation of $\sigma = 0.35$ meters. So, with respect to giraffes’ heights, a giraffe that is 5.5 meters tall has a z-score of:
$z(5.5) = \dfrac{5.5 – 5}{0.35}$
$= \dfrac{0.5}{0.35} = 1.43$
Men’s heights are (approximately) normally distributed with a mean of $\mu = 70$ inches and a standard deviation of $\sigma = 3$ inches. So, with respect to men’s heights, a man that is 2.0 meters (6 feet 7 inches = 79 inches) tall has a z-score of:
$z(79) = \dfrac{79 – 70}{3}$
$= \dfrac{9}{3} = 3.00$
So that 2 meter tall man (z-score of 3.00) is relatively speaking, much taller than that 5.5 meter giraffe (z-score of 1.43).
Proof of the z-transformation theorem. Optional!
(This is only for the students who have taken Calculus)
The z-transformation theorem (statement):
If
$$x \sim N(\mu_x, \sigma_x)$$
then
$$z(x) = \dfrac{x – \mu_x}{\sigma_x}$$
is $N(0,1)$ and
$$P(a < x < b) = P(z(a) < z < z(b))$$
Sketch of proof: If $x \sim N(\mu_x, \sigma_x)$ the PDF for $x$ is given by:
$$f(x) = \frac{1}{\sigma_x \sqrt{2 \pi}}\,\text{e}^{-\dfrac{(x-\mu_x)^2}{2 \sigma_{x}^{2}}}$$
and
$P(a < x < b)$
$\displaystyle = \int_{a}^{b} \frac{1}{\sigma_x \sqrt{2 \pi}}\,\text{e}^{-\dfrac{(x-\mu_x)^2}{2 \sigma_{x}^{2}}} \, dx $
$\displaystyle = \int_{z(a)}^{z(b)} \frac{1}{\sqrt{2 \pi}}\,\text{e}^{-\dfrac{z^2}{2 }} \, dz$
$=P(z(a) < z <z( b))$
In the above, the equality of integrals is due to the change-of-variables theorem, i.e., u-substitution, except instead of using the letter u we are using the letter z, with
$$z(x) = \dfrac{x – \mu_x}{\sigma_x}$$
Finding areas (probabilities) for
$\mathbf{x \sim N(\mu_x, \sigma_x)}$
using the z-distribution and the z-transformation theorem
Question 16. Suppose $x$ is $N(100,10)$. Find $P(93 < x < 114 )$. Draw $x$ and shade the region corresponding to $P(93 < x < 114 )$.
Answer to Question 16.
We will solve this problem two ways.
- Using the z-transformation theorem together with the z-table. This is the traditional way to solve such problems.
- Using R
Method 1. To solve Question 16: apply the z-transformation:
$z(x) = \dfrac{x – \mu_x}{\sigma_x} = \dfrac{x – 100}{10} $
and then use the z-table.
$P(93 < x < 114) $
$=P(z(93) < z(x) < z(114))$
$=P\left(\dfrac{93 – 100}{10} < z < \dfrac{114 – 100}{10}\right)$
$=P\left(\dfrac{-7}{10} < z < \dfrac{14}{10}\right)$
$=P\left(-0.70 < z < 1.40\right)$
$= A(1.40) – A(-0.70)$
$ = .9192 – .2420$
$ = .6772$

The above Figure shows the region corresponding to $P(93 < x < 114 )$ shaded green.
Method 2. Using R.
If we use R, we can avoid using the z look up table. If $x \sim N(\mu_x, \sigma_x)$ then
$P(x < b) = \text{pnorm}(b, \mu_x, \sigma_x)$
where “pnorm” is R’s normal distribution probability function.
$P(93 < x < 114) $
$= P(x < 114) – P(x < 93)$
$= 0.9192433 – 0.2419637$
$= 0.6772797$
We found $P(x < 114)$ and $P(x < 93)$ using the following R script.
# P(a < x < b) if x is N(mu_x, sigma_x) a = 93 b = 114 mu_x = 100 sigma_x = 10 #----------------- no need to change anything below this line pnorm(b, mu_x, sigma_x); pnorm(a, mu_x, sigma_x); pnorm(b, mu_x, sigma_x) - pnorm(a, mu_x, sigma_x); #the above number is P(a < x < b) # End of script

The following R script produced the above Figure solving Question 16.
# P(a < x < b) without using z transformation
# Draw PDF of x is N(mu_x, sigma_x)
# Shade region corresponding to P(a < x < b)
mu_x = 100; # population mean of x
sigma_x = 10; # population standard deviation of x
a = 93;
b = 114;
#---------------------------------------------------------
# No need to change anything below this line.
#---------------------------------------------------------
Pa = pnorm(a,mu_x, sigma_x );
Pb = pnorm(b,mu_x, sigma_x )
Pab = pnorm(b,mu_x, sigma_x ) - pnorm(a,mu_x, sigma_x );
sds = 3.5;
xvals = seq(mu_x - sds*sigma_x, mu_x + sds *sigma_x, by = 0.001);
pdf = dnorm(x = xvals, mean = mu_x, sd = sigma_x);
xtickmarks = seq(mu_x - 2*sigma_x, mu_x + 2*sigma_x,sigma_x);
plot(xvals, pdf, type = "l", lwd = 3,
ylab = "probability density",
xlab = "x",
col = "black",
ylim = c(0, max(pdf)),
xaxt='n',
main = paste("x is N(",mu_x,",",sigma_x,"). ", "P(",a,"< x <",b,") = P(x < ", b,") - P(x < ",a,
") \n \ \ = ",
sprintf('%.5f',Pb), " - ", sprintf('%.5f',Pa) , " = " , sprintf('%.4f',Pb - Pa), " " ) );
axis(side = 1, at = xtickmarks ,labels = T);
xShade = seq(a, b, by = sigma_x/50);
pdfShade = dnorm(x = xShade, mean = mu_x, sd = sigma_x);
polygon(c(xShade,rev(xShade)),c(pdfShade,0*rev(pdfShade)),col="green");
lines(c(min(xvals)- abs(min(xvals)),
max(xvals)+ abs(max(xvals))),
c(0, 0),
col = "black", lwd = 3);
lines(c(mu_x,mu_x), c(0,1.1*dnorm(mu_x, mu_x, sigma_x)), lty = "dashed");
pnorm(b,mu_x, sigma_x ) - pnorm(a,mu_x, sigma_x )
# above numer is P(a < x < b)
# End of script
The above R script can be copied and pasted into R on your computer, or run online at:
- https://rdrr.io/snippets/
- https://repl.it/languages/rlang
(If you run the R script in repl.it, to see the graph you have to click on the left side of the webpage, where it says “Rplots.pdf”.)
Standard Normal Distributions Questions
for Homework and Quizzes
(Questions 17 to 20)
Question 17.0. If $A(z) = .0028$, what does $z$ equal? Use the z-table.
Answer to Question 17.0. $z = -2.77$ (answer). See Figure below.

Question 17.1. If $A(z) = .8508$, what does $z$ equal? Use the z-table.
Answer to Question 17.1. $z = 1.04$ (answer). See Figure below.

z-score Questions
For $x \sim N(\mu_x, \sigma_x)$ the z-score formula is $z(x) = \dfrac{x – \mu_x}{\sigma_x}$
Question 18.0. If $x \sim N(38, 4)$ find the z-score of $x = 39$. In other words find $z(39)$.
Answer to Question 18.0.
Since $x \sim N(38, 4)$ we know that $\mu_x = 38$ and $\sigma_x = 4$. Then we use the z-score formula.
$z(x) = \dfrac{x – \mu_x}{\sigma_x}$
$z(39) = \dfrac{39 – 38}{4} = \dfrac{1}{4} = 0.25$
So, the z-score is 0.25 (answer).
Question 18.1. If $x \sim N(-10, 4)$ find the z-score of $x = -8$. In other words find $z(-8)$.
Answer to Question 18.1.
Since $x \sim N(-10, 4)$ we know that $\mu_x = -10$ and $\sigma_x = 4$. Then we use the z-score formula.
$z(x) = \dfrac{x – \mu_x}{\sigma_x}$
$z(-8) = \dfrac{-8 – (-10)}{4} = \dfrac{-2}{4} = -0.50$
So, the z-score is 0.50 (answer).
Question 18.2. If $x \sim N(10, 6)$ find the z-score of $x = 8$. In other words find $z(8)$.
Answer to Question 18.2.
Since $x \sim N(10, 6)$ we know that $\mu_x = 10$ and $\sigma_x = 6$. Then we use the z-score formula.
$z(x) = \dfrac{x – \mu_x}{\sigma_x}$
$z(8) = \dfrac{8 – 10}{6} = \dfrac{-2}{6} = -0.33$
So, the z-score is -0.33 (answer).
Question 19. Suppose that men’s heights are normally distributed with a mean of 70 inches and standard deviation of 3 inches. Find the probability that a randomly selected man will be taller than 6 feet (72 inches).
Answer to Question 19.
Let $x$ be the random variable that measures men’s heights. So, $\mu_x = 70$ inches and $\sigma_x = 3$ inches. In inches: $x \sim N(70, 3)$.
Using the z-table and z-transformation theorem
Since $x \sim N(70, 3)$ the z-transformation (or z-score) formula is:
$z(x) = \dfrac{x – \mu_x}{\sigma_x}$
$ = \dfrac{x – 70}{3}$
so
$z(72) = \dfrac{72 – 70}{3}$
$= \dfrac{2 }{3} \approx 0.67$
However, it is quicker to put the z-score calculation directly into the probability calculation, as I do here:
$P(72 < x) $
$=1 – P(x<72)$
$=1 – P(z(x) < z(72))$
$=1 – P\left(z < \dfrac{72 – 70}{3}\right)$
$=P\left(z < \dfrac{2}{3}\right)$
$=P\left(z < 0.67\right)$
$= 1 – A(0.67)$
$ = 1 – .7486$ (from z-table)
$ = .2514$ (answer)
Using R’s pnorm command

$P(72 < x) $
$=1 – P(x<72)$
$=1 – \text{pnorm}(72, \mu_x = 70, \sigma_x = 3)$
$=1 – 0.7475075$
$= 0.2524925$ (answer)
Note about accuracy. R’s answer is more accurate than what we got using the z-table method. This is because we had to round $z(72) = 2/3 = 0.6666\ldots$ to $0.67$ in order to use the z-table. R doesn’t round as much.
Historical note. The z-table method was the only practical way to find normal distribution probabilities until computers were invented. A table which could easily be converted to our z-table was published in 17991 by Christian Kramp. Each entry in that table was the result of a laborious calculation done by Kramp. In most statistics textbooks the z-table method is still emphasized. One reason for this is that most handheld calculators don’t have a pnorm function like R’s and students typically aren’t allowed to use computers to take statistics exams.
Warning! In my online statistics classes I use R to calculate the answers to your homework and quiz questions. So, on quizzes and homework, for normal distribution questions, unless you are explicitly told to use the z-table (like for Question 17.0 and 17.1) you should use R to find the numerical answer.
Question 20. Suppose that men’s heights are normally distributed with a mean of 70 inches and standard deviation of 3 inches. Find the probability that a randomly selected man will be between 5 feet 6 inches (66 inches) and 6 feet (72 inches) tall.
Answer to Question 20.
Let $x$ be the random variable that measures men’s heights. So, $\mu_x = 70$ inches and $\sigma_x = 3$ inches. In inches: $x \sim N(70, 3)$.
Using the z-table and the z-transformation theorem
$P(66 < x < 72) $
$=P(z(66) < z(x) < z(72))$
$= P\left(\dfrac{66 – 70}{3} < z < \dfrac{72 – 70}{3}\right)$
$=P\left(\dfrac{-4}{3} < z < \dfrac{2}{3}\right)$
$=P\left(-1.33 < z < 0.67\right)$
$= A(0.67) – A(-1.33)$
$ = .7486 – .0918$ (from z-table)
$ = .6568$ (answer)
Using R’s pnorm command

$P(66 < x < 72) $
$= P(x < 72) – P(x < 66)$
$= \text{pnorm}(72, \mu_x = 70, \sigma_x = 3) $
$- \text{pnorm}(66, \mu_x = 70, \sigma_x = 3) $
$= .7475075 – 0.09121122 $
$= 0.6562962$ (answer)
- (2005) Tables Related to the Normal Distribution, The American Statistician, 59:4, 309-311, DOI: 10.1198/000313005X70911

